代数的位相幾何学
幾何学における基本的手法の概略を把握するこ とを目標に、モース理論・代数的位相幾何学・ リー群論・リーマン幾何学に関する基本的事項 について解説する。 01b6423, 0aja021と同 一。 要望があれば英語で授 業 01bb004幾何学概論ii 1 3.0 1・2 秋abc 水・金3 1e503.

代数的位相幾何学. 代数多様体 はアフィン 代数多様体 の張り合わせで作られるようなので、ここではアフィン 代数多様体 の定義を示しておく 1。. 教 授 博士(理学) 成瀬 慶明. My Favorite Textbooks 代数学や位相幾何学における各科目についての参考書に関する質問を,学生からあまりにも何度も受けるのでここに纏めることにいたしました.以下は私の経験(主に学生の頃に実際に読んでいたもの)に基づくもので,決してこれ以外に良いものがないということではあり.
代数的位相幾何学における局所化原理 Serre の C 理論 Morava による複素コボルディズム論の局所化 Morava K-theory Geometric localization theorem M.J.Hopkins 1980年代後半 球面のホモトピー の有限性 Adams のスペクトル列 Toda の Composition method. 教員名:糸 健太郎(いと けんたろう) 2. 17-10 57 統計的モデリングと予測理論のための統合的数理研究 10.
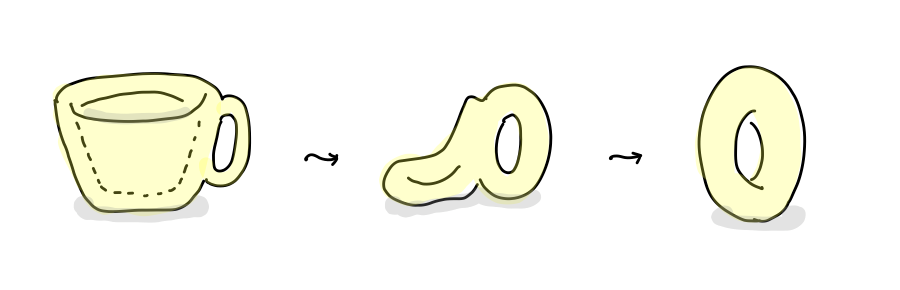
トポロジーと幾何学 編集 位相空間論 編集. 代数的位相幾何学(だいすうてきいそうきかがく、英語:algebraic topology、代数的トポロジー)は代数的手法を用いる位相幾何学の分野のことをいう。 古典的な位相幾何学は、図形として取り扱い易い多面体を扱っていたが、1900年前後のポアンカレの一連の研究を契機として世紀に発展した 。. 代数的位相幾何学は位相空間を調べるのに抽象代数学由来の道具を用いる数学の一分野である 。 その基本的な最終目的は 同相 を除いて 位相空間を分類する代数的 不変量 を求めることであるが、普通は ホモトピー同値 を除いて大まかな分類を得ることが目的となる。.
非可換代数幾何学 221 ることに対応する. Gelfand–Kirillov次元が0の整域はk のみであることはすぐに分かる(ここで非可換の場合でも可 換の場合と同様に,整域とは0以外の零因子を持たない環をさす).これは次元0の(既約) 多様体は 一点のみからなることに対応している.次のSmall–Warfieldの結果. フリー百科事典『ウィキペディア(Wikipedia)』 ( 09:27 UTC 版) 代数的位相幾何学(だいすうてきいそうきかがく、英語:algebraic topology、代数的トポロジー)は代数的手法を用いる位相幾何学の分野のことをいう。 古典的な位相幾何学は、図形として取り扱い易い多面体を扱っていた. この位相を のザリスキ位相 (Zariski topology) という.
所属 (過去の研究課題情報に基づく):九州大学,数理学研究院,教授, 研究分野:代数学,代数学・幾何学,代数学, キーワード:保型形式,モジュラー形式,保型関数,代数的組合せ論,アソシエーションスキーム,コード,code,spherical design,有限体,超幾何関数, 研究課題数:25, 研究成果数:34. 大まかに言うと、cの上の代数幾何学で正しいステートメントは、任意の標数が 0 である代数的閉体の上でも正しいということである。 詳細な原理の証明は、 アルフレト・タルスキ (Alfred Tarski)により、 数理論理学 を基礎としてなされた。. 表示的意味論のために位相束が研究されて領域理論が作られたのは, もはや昔話になりつつありますが, 近年でも, 並列プログラムの解析に代数的位相幾何学の方法が用いられる, 高階論理 (型理論) のモデル構成に圏論的普遍代数の方法が用いられるなど.
17-10 58 非圧縮性粘性流体の数理解析 13. 代数幾何学 の主要な研究対象は 代数多様体 である。. 具体的には、 X 内の道のホモトピーあるいは道ホモトピー (path-homotopy) とは、 I で添字付けられた X.
上で説明した結び目理論や3次元多様体論は、位相幾何学の一分野ですから、もちろん位相幾何学的な手法を用いて研究ができます。ここでいう量子位相幾何学(quantum topology)は、1984年に発見された Jones 多項式から始まるものです。. *2 代数的 集合という. アフィン 代数多様体 (古典的定義) の既約な 閉集合 にザリスキ位相から誘導された位相を入れたものをアフィン 代数多様体 (affine.
世界大百科事典 第2版 - 代数的位相幾何学の用語解説 - 位相不変量として次元の概念を設定する問題と方法は,今世紀のはじめにポアンカレにより提示されたが,l.e.ブローエルらによる数学的定式化を経て,今日ほぼ完成の域に達している。ホモトープ,ホモローグの概念は,今世紀前半を通じ. 代 数 的 な 道 具 コホモロジ ー 作 用. あり,代 数的位相幾何学における一般コホモロジーと類似の性質をもっている.一 般コホモロジー が代数的位相幾何学に革新をもたらしたのと同じように,代 数的κ理論は整数論,代 数幾何学, Geornetric topologyな どの諸分野に適用され,重 要な成果を収めつつある.
幾何学における基本的手法の概略を把握するこ とを目標に、モース理論・代数的位相幾何学・ リー群論・リーマン幾何学に関する基本的事項 について解説する。 01b6423, 01bb003と同 一。 要望があれば英語で授 業 0aja022幾何学概論ii 1 3.0 1・2 秋abc 水・金3 1e503. 兵庫教育(ひょうごきょういく)大学公式サイト。兵庫県加東市にキャンパス。学校教育学部、大学院修士課程、大学院専門職学位課程(教職大学院)、大学院博士課程(連合大学院)を擁する国立の教員養成大学。略称は兵教大。英文表記は、Hyogo University of Teacher Education。. 位相空間論において、埋め込みとは、像の上への同相写像のことである 。 つまり、位相空間 X と Y の間の単射 連続写像 f:.
教授 (代数的位相幾何学、数理物理) 本多 宣博:. 代数的位相幾何学(だいすうてきいそうきかがく、英語:algebraic topology、代数的トポロジー)は代数的手法を用いる位相幾何学の分野のことをいう。 古典的な位相幾何学は、図形として取り扱い易い多面体を扱っていたが、1900年前後のポアンカレの一連の研究を契機として世紀に発展した。 ポアンカレは 15年に出版した "Analysis Situs" の中で、ホモトピーおよび. 教授 (微分幾何学) カールマン タマシュ:.
数学において、ホモトピー群は 位相空間 を分類する為に代数的位相幾何で用いられる.最初のかつ最も単純なホモトピー群は 基本群 であり、これは空間のループに関する情報を記録している。. 代数的位相幾何学(だいすうてきいそうきかがく、英語:algebraic topology、代数的トポロジー)は代数的手法を用いる位相幾何学の分野のことをいう。 古典的な位相幾何学は、図形として取り扱い易い多面体を扱っていたが、1900年前後のポワンカレの一連の研究を契機として世紀に発展した 。. 教授 (位相幾何学) 五味 清紀:.
位相幾何学 (いそうきかがく、 topology ;. 教 授 博士(理学) 佐野 友二. 教授 (複素幾何、微分幾何) 山田 光太郎:.
代数的位相幾何学 は、 ホモロジー群 や ホモトピー群 などの代数的構成を用いて連結性の度合いを測ることを試みる。 微分位相幾何学 は 可微分多様体 上の 可微分写像 を扱う分野である。.

英語数学洋書 Algebraic Topology 代数的位相幾何学 Edwin H Spanier マグロウヒル の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版
講師列伝 代数的位相幾何学 リード予備校 岐阜 リード進学塾 リード予備校

拓扑学 维基百科 自由的百科全书
代数的位相幾何学 のギャラリー

代数的位相幾何学入門 上 旧装丁 W フルトン 三村護訳 明倫館書店 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋

トポロジーは 人の知能 知性の本質とつながっているように感じます 奈良女子大学小林教授が語る位相幾何学 Lab On 研究の未来をデザインするメディア

代数的位相幾何学 1975年 感想 レビュー 読書メーター

代数的位相幾何学入門 上 W フルトン 三村 護 本 通販 Amazon

ヤフオク 笹尾靖也 著 代数的位相幾何学 森北出版

More Concise Algebraic Topology Localization Completion And Model Categories Chicago Lectures In Mathematics May J P Ponto K 紀伊國屋書店ウェブストア オンライン書店 本 雑誌の通販 電子書籍ストア
大学数学系 南开大学数学系 山东大学数学系 哈佛大学数学系

複素代数幾何学入門堀川穎二 著岩波書店 書込 個人印あり 爱买 Imaijp 日本代购网

Tokyo Sanovabitch Topology

Q Tbn 3aand9gcrcus44gby4kk5zaknz Jrhh8hefyjrimcctg Usqp Cau
2

位相幾何学の値段と価格推移は 30件の売買情報を集計した位相幾何学の価格や価値の推移データを公開
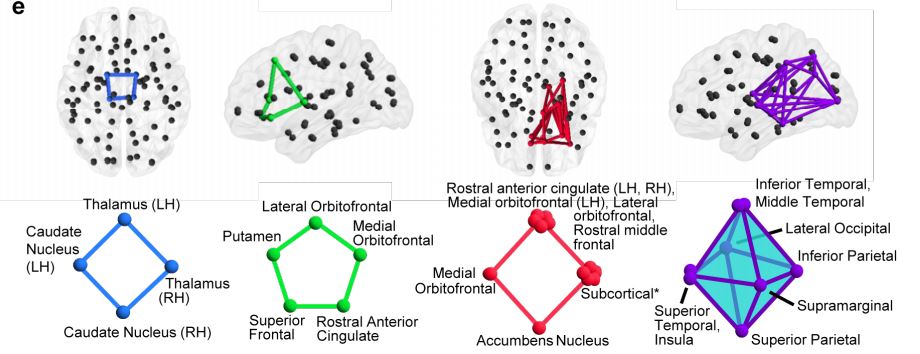
Mit Tech Review コネクトーム 脳の構造を代数的位相幾何学で理解できることが判明

英語数学洋書 Algebraic Topology 代数的位相幾何学 Edited By Arunas Liulevicius 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋

哆嗒数学网 博客

錐 位相幾何学 Wikipedia

幾何学的トポロジー Wikipedia

春の代数的位相幾何学セミナー 17

位相幾何学入門 ホモロジー群の計算 Youtube

代数的位相幾何学入門 上 Amazon Com Books

結城浩 今日の圏論 圏論の基礎 代数的位相幾何学における関手の例として次元nの特異ホモロジーの話 位相空間と連続写像をアーベル群と準同型に移す関手 Top Ab 数学ガールでよく出てくる世界と世界の橋渡しだ

道 位相幾何学 Wikipedia

数学の幾何的様相 神戸大学先端融合研究環 自然科学 生命医学系融合研究領域
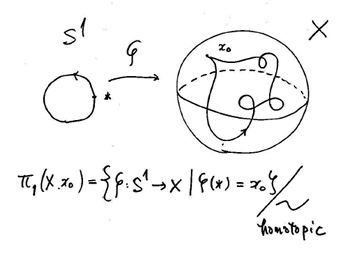
空間の代数的模型 圏を行き来して幾何学的対象を理解する 理学クエスト ようこそ 探求の世界へ 信州大学 理学部

Category 代数的位相幾何学の定理 Page 1 Japaneseclass Jp

代数的位相幾何学の通販 笹尾 靖也 紙の本 Honto本の通販ストア

ブルバキ数学言論 6冊 精解演習 4冊 技術者のための高等数学 4冊 計14冊 Buyee Buyee 提供一站式最全面最专业现地yahoo Japan拍卖代bid代拍代购服务

转载 代数 几何 分析各自的范畴或者说三者到底有什么不同 知乎

ヤフオク 笹尾靖也 著 代数的位相幾何学 森北出版

大学数学系学什么 尚书坊
2
幾何学 Wikipedia

代数的位相几何学 搜索结果 哔哩哔哩弹幕视频网 つロ乾杯 Bilibili

代数的位相幾何学入門 Fulton William 著 シュプリンガー フェアラーク東京 版元ドットコム

代数的位相幾何学入門 下 W フルトン 三村 護 本 通販 Amazon

メンバー紹介

ヤフオク 笹尾靖也 著 代数的位相幾何学 森北出版

代数的トポロジー 代数的位相幾何学 の講義ノートpdf ホモトピー ホモロジーを使った幾何の入門 主に言語とシステム開発に関して

代数的トポロジー 代数的位相幾何学 の講義ノートpdf ホモトピー ホモロジーを使った幾何の入門 主に言語とシステム開発に関して

代数的位相幾何学入門 上 W フルトン 三村 護 本 通販 Amazon
幾何学 代数学

拓扑学 Wikiwand
2

多次元にもほどがある 人間の脳は最大11次元の構造を持つ可能性 代数的位相幾何学 17年6月日 エキサイトニュース

英語数学洋書 Algebraic Topology 代数的位相幾何学 Edwin H Spanier マグロウヒル の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版

京都大学 纪和留学

結城浩 今日の圏論 圏論の基礎 代数的位相幾何学における関手の例として次元nの特異ホモロジーの話 位相空間と連続写像をアーベル群と準同型に移す関手 Top Ab 数学ガールでよく出てくる世界と世界の橋渡しだ

楽天ブックス 代数的位相幾何学入門 上 ウィリアム フルトン 本

ヤフオク 笹尾靖也 著 代数的位相幾何学 森北出版

代購代標第一品牌 樂淘letao 英語数学洋書algebraic Topology 代数的位相幾何学 アメリカ数学会 Contemporary Mathematics 96

英語数学洋書 Algebraic Topology 代数的位相幾何学 Edited By Arunas Liulevicius 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋

ヤフオク 笹尾靖也 著 代数的位相幾何学 森北出版

代数的位相幾何学入門 上下巻 全2冊 W フルトン著 三村護訳 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋
脳 人間の脳の構造は最大11次元 代数的位相幾何学を用いた分析結果 スイス研究 サイバーニュース

数学词汇大全 百度文库
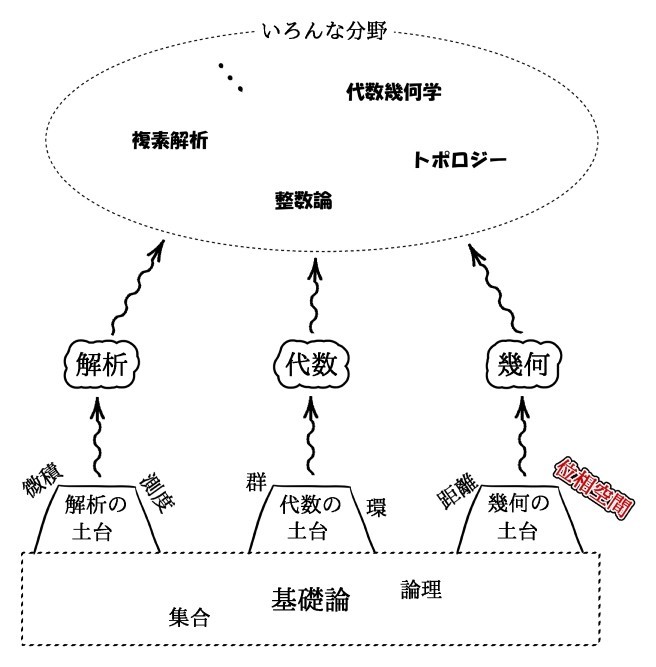
大学数学の難関分野 位相空間論 とは一体何なのか きいねく Note

79i 代数的位相幾何学 笹尾靖也 著 Br 数学全書9 森北出版

代購代標第一品牌 樂淘letao 英語数学洋書algebraic Topology 代数的位相幾何学 アメリカ数学会 Contemporary Mathematics 96
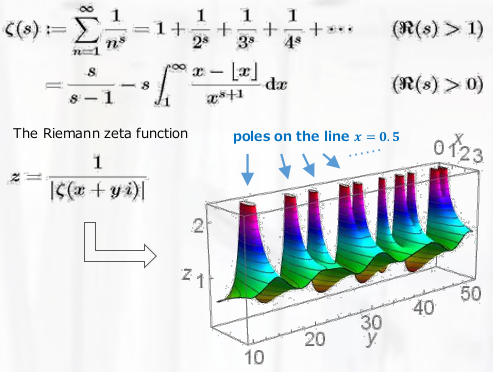
代数的位相幾何学 Algebraic Topology Japaneseclass Jp

79i 代数的位相幾何学 笹尾靖也 著 Br 数学全書9 森北出版

代数的位相幾何学入門 下 W フルトン Hmv Books Online

ヤフオク 笹尾靖也 著 代数的位相幾何学 森北出版

複素代数幾何学入門堀川穎二 著岩波書店 書込 個人印あり 爱买 Imaijp 日本代购网

代数的位相幾何学入門 上 フルトン w 著 fulton william Amazon Com Books

傲览千古a Twitter 对于这个用初等三角代数函数所描述的超自然的 超现实的 纯粹理想的 最普遍的 最抽象的 最一般的波动曲线方程式 在这门非线性的 二维初等波浪点集平面几何学 中 可引进 两大类四种不同的连续正变换群 对该方程式加以简化 获得这种最

代数的位相幾何学 タグ記事一覧 Mitテクノロジーレビュー

代数的位相幾何学入門 上 W フルトン 三村 護 本 通販 Amazon

代数拓扑 集合拓扑 代数拓扑 拓扑关系 拓扑结构 笔记 Web开发 亿速云

代購代標第一品牌 樂淘letao 英語数学洋書algebraic Topology 代数的位相幾何学 アメリカ数学会 Contemporary Mathematics 96

代数的位相幾何学

代数的位相幾何学入門 上下巻 全2冊 W フルトン著 三村護訳 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋

ヤフオク 位相幾何学 の落札相場 落札価格

楽天ブックス 代数的位相幾何学入門 下 ウィリアム フルトン 本
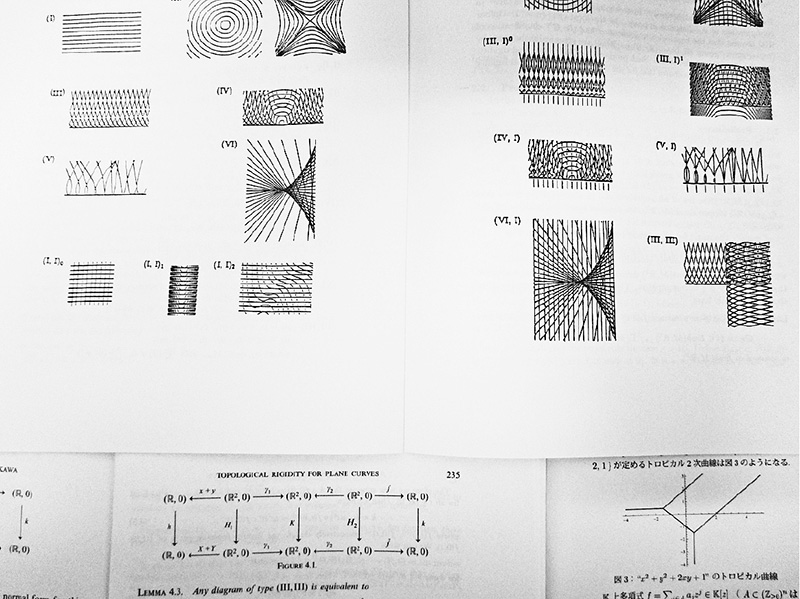
位相幾何学研究室 芝浦工業大学

ヤフオク 笹尾靖也 著 代数的位相幾何学 森北出版

代数的位相幾何学入門 下 w フルトン 著 三村 護 訳 本 オンライン書店e Hon

ブルバキ数学言論 6冊 精解演習 4冊 技術者のための高等数学 4冊 計14冊 Buyee Buyee 提供一站式最全面最专业现地yahoo Japan拍卖代bid代拍代购服务

代数的トポロジーを治療に用いる 深く潜れ Dive Deep キネシオロジー クラニオセイクラル ワーク クラニオ の蒼穹堂治療室

英語数学洋書 Algebraic Topology 代数的位相幾何学 Mark Mahowald Stewart Priddy 編 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋

講師列伝 代数的位相幾何学 リード予備校 岐阜 リード進学塾 リード予備校

可換環論bot 代数幾何は とても堅い トポロジーは やわらかい 幾何学と言われます この間に微分幾何や解析幾何 など 一般に 幾何学 と呼ばれる分野があります 代数幾何学は 代数学 に分類されがち トポロジーは突き抜けてやわらかいので幾何学

幾何学の古書の高価買取なら藍青堂書林 全国対応 専門書買取専門店 藍青堂書林 10冊以上で宅配送料無料

位相幾何学クイズ その1 現実と数学の区別が付かない

7d Simplex 代数的位相幾何学 神経の接続は最高で11次元になる 幾何学アート 位相幾何学 ストリングアート

英語数学洋書 Algebraic Topology 代数的位相幾何学 Mark Mahowald Stewart Priddy 編 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋
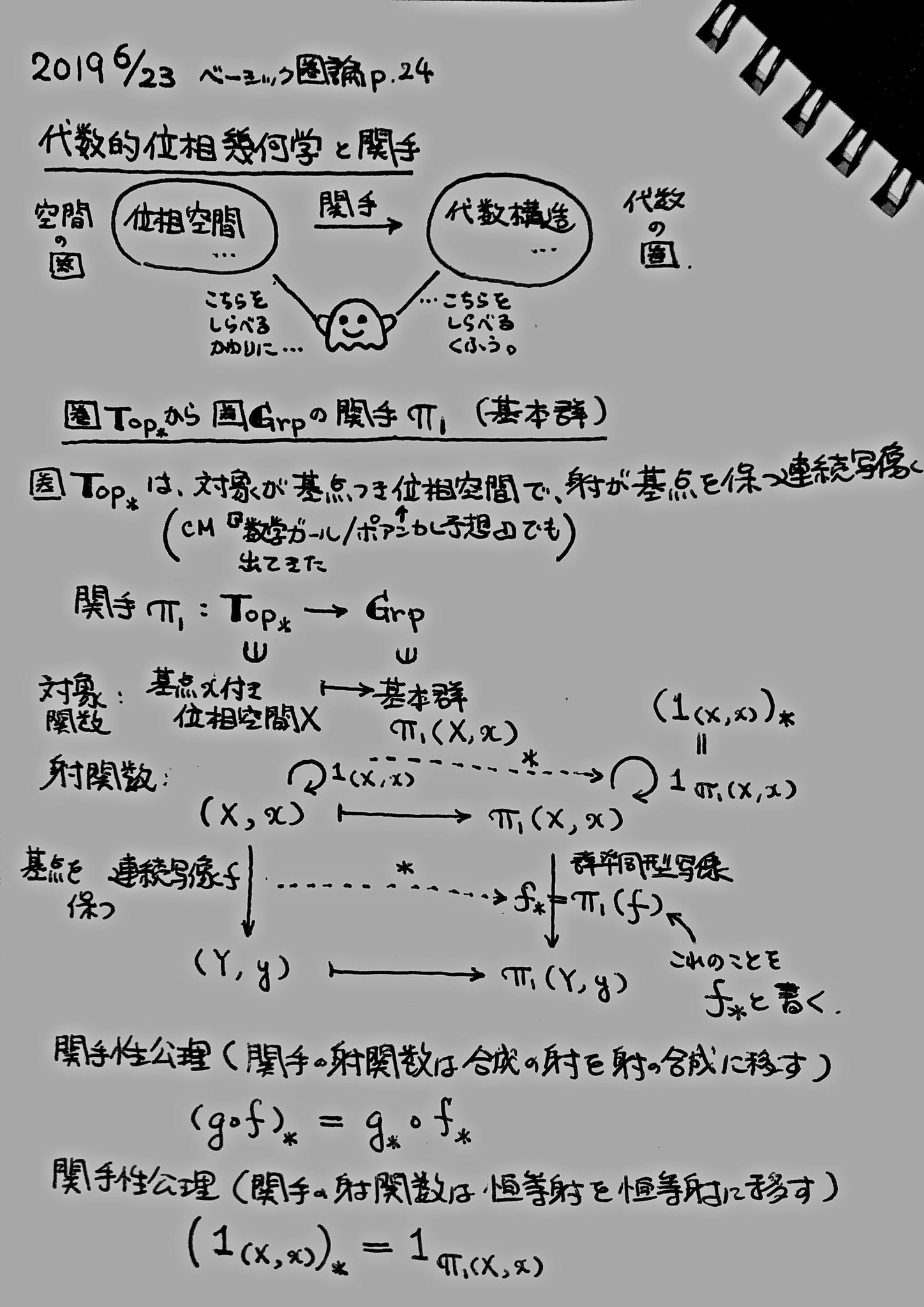
代数的位相幾何学と関手 結城浩の圏論勉強プロジェクト

英語数学洋書 Symposium On Algebraic Topology シンポジウム 代数的位相幾何学 Edited By Peter J Hilton 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋

きょうと数学勉強会 大学院生時代は代数トポロジーです 代数的位相幾何学とも呼びます 名前は似ていますが代数幾何は ほとんど知らないので恐れをなしてしまいます ハーツホーン読みたい とはことあるごとに言っていたりします Peing 質問箱

英語数学洋書 Algebraic Topology 代数的位相幾何学 Edwin H Spanier マグロウヒル の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版
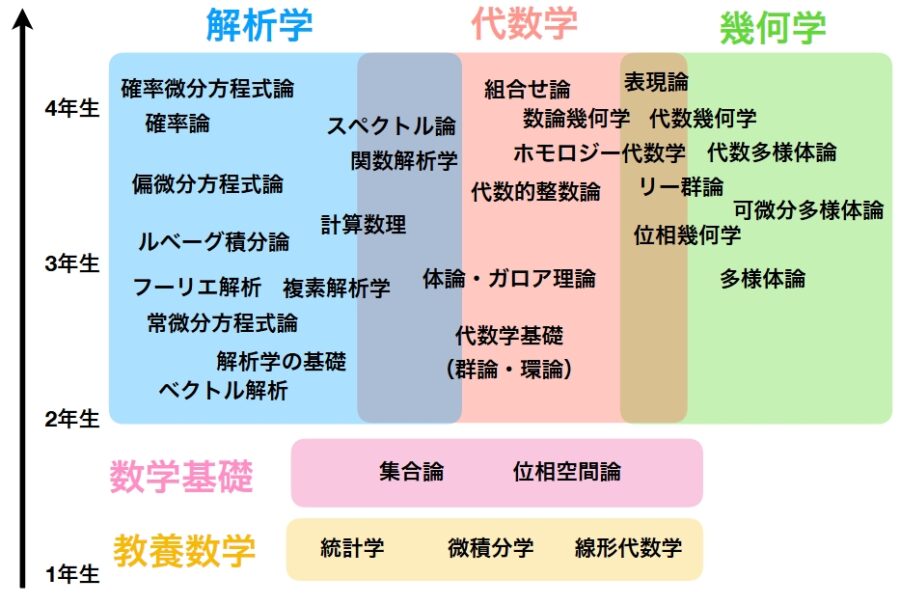
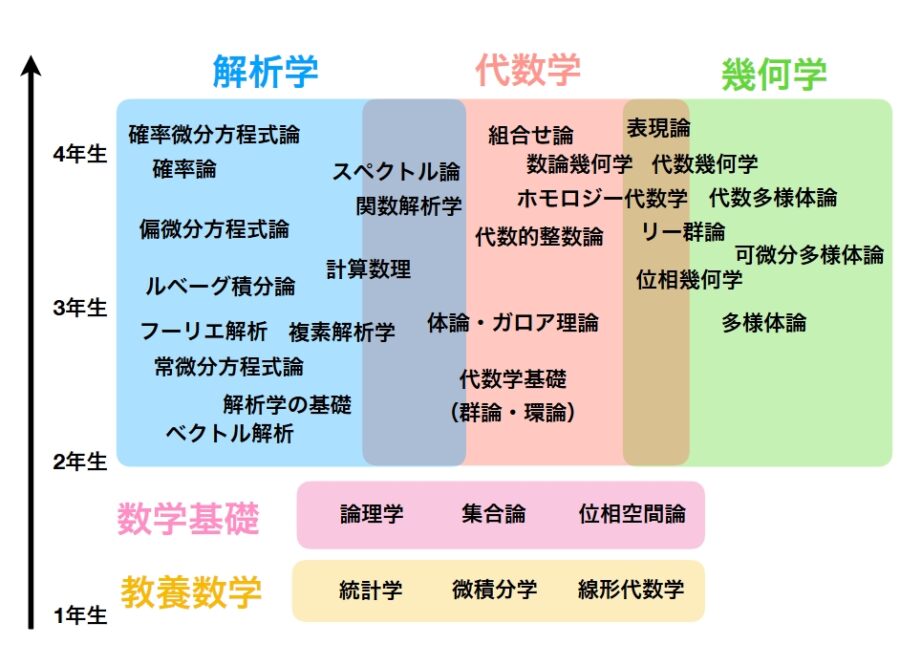
大学数学のロードマップ 分野一覧と学ぶ順序 趣味の大学数学

ヤフオク 笹尾靖也 著 代数的位相幾何学 森北出版
現代代数学と異分野連携研究部門 東京理科大学研究推進機構総合研究院

Lectures On Introduction To Algebraic Topology 英 代数的位相幾何学入門講義 G De Rham ド ラーム 明倫館書店 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋
Advent Pdf Google Drive
2

数学で割り出した脳モデルで明らかに 人間の脳は最大11次元の構造を持っている スイス研究 カラパイア 人間の脳 位相幾何学 代数

ヤフオク 笹尾靖也 著 代数的位相幾何学 森北出版



